研究を始める時に避けては通れないものが統計解析です。
もちろん研究者は統計のスペシャリストではありませんから、ここで躓く人も多いのではないでしょうか?
「自分の研究でどんな統計解析の方法を使ったらいいか分からない」
「統計解析の手法が多すぎて、違いがわからない」
などといった悩みをお持ちの方も多いはずです。
本記事は研究をする上で最低限必要な統計解析の手法をまとめています。
これらの手法を知っていれば、ほとんどの研究に対応可能です。
統計解析でお悩みの方はぜひご活用くださいね!
介入研究(RCT)でよく使う統計解析
異なる2群の差をみたい場合
異なる2群の差をみる解析は以下の方法があります。
- 対応のないt検定(データが正規分布している場合)
- マンホイットニーのU検定(データが正規分布していない場合)
- カイ二乗検定(データが2値変数の場合)
いずれも異なる2群の差をみる解析ですが、データの種類によってどの手法を使うか変わってきます。
T検定はデータが正規分布している場合に使うことができる、最もメジャーな統計解析手法です。
正規分布しているデータとは、分布が下図のようになるデータです。
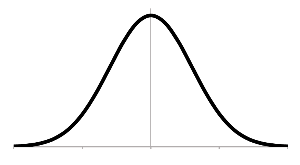
正規分布を簡単に説明すると「平均値付近であるほど多く、平均値から外れるほど少なくなるデータ」です。
身長や体重、50m走のタイムなど、正規分布に当てはまるものが多いです。
差を比較したいデータが正規分布していなかった場合は、マンホイットニーのU検定を使います。
データを順位に変換した後に解析をするため、データがどんな分布でもある程度の精度で解析できるという特徴を持っています。
データが2値変数の場合は、カイ二乗検定を使いましょう。
2値変数とは、「有」「無」や「男」「女」などの2種類しかないデータのことです。
たとえば異なる2群である病気の発症率の差(「発症」「未発症」の2値データ)をみたい場合などでカイ二乗検定を使用します。
基本的に異なる2群の差をみたい時に使う統計手法は以上の3つだけです。
異なる3群以上の差をみたい場合
異なる3群以上の差をみる解析は以下の方法があります。
異なる2群の差をみる解析は以下の方法があります。
- 繰り返しのある一元配置分散分析(データが正規分布している場合)
- クラスカルワリス検定(データが正規分布していない場合)
- カイ二乗検定(データが2値変数の場合)
手法の名前が変わるだけで、基本的には2群比較の時と同じです。
カイ二乗検定は2群でも3群でも使えます。
差を比べるデータが正規分布しているか?2値変数ではないか?を確かめて該当する手法を使用しましょう。
ただし注意点があります。
今紹介した手法は”比較した群のいずれかの間に差がある”ことを検定するだけで、どの群とどの群に差があるのかまでは分かりません。
どの群とどの群に差があるのか詳しく知りたい場合は、多重比較と呼ばれる追加解析が必要になります。
多重比較には以下の方法があります。
- Tukey-Kramer法(データが正規分布している場合)
- Steel-Dwass法(データが正規分布していない場合)
- ボンフェロー二調整をかけて各群同士でカイ二乗検定(データが2値変数の場合)
ボンフェローニ調整について詳しく説明しておきましょう。
ボンフェローニ調整とは繰り返し検定をかけた回数分、p値を補正することです。
たとえばA群、B群、C群の3群でカイ二乗検定を実施し、有意差が出たとしましょう。
この時点ではまだどの群とどの群に差があったのか分かりません。
そこでA群×B群、B群×C群、C群×A群でそれぞれカイ二乗検定を行っていくのですが、算出されるp値にボンフェローニ調整をかけなければなりません。
算出されたp値がそれぞれ「0.01,0.04,0.10」であれば、それぞれに検定を繰り返した数(今回は3回)だけ掛け算し、「0.01×3,0.04×3,0.10×3」とします。
ボンフェロー二調整前であればB群×C群で有意差がありましたが、ボンフェローニ調整後は有意ではなくなりましたね。
実際にボンフェローニ調整を行う際は以下の表だけ覚えておけばOKです。
3群→p値×3
4群→p値×6
5群→p値×10
繰り返し検定をかける場合は、その数だけ有意水準を厳しくなるということを覚えておきましょう。
介入前と介入後の差をみたい場合
今までは異なる群の差をみる場合の解析手法を紹介してきました。
でも同じ群を対象にして介入前と介入後の差をみたい場合もありますよね。
その場合の解析手法は以下の通りです。
- 対応のあるt検定(データが正規分布している場合)
- ウィルコクソンの符号順位検定(データが正規分布していない場合)
- マクネマー検定(データが2値変数の場合)
手法の名前が変わるだけで、基本的には2群比較の時と同じです。
異なる2群を比較する解析手法との違いは、同じ人の変化量を比較しているという点です。
対応のないt検定では2群の平均値同士を比較するだけですが、対応のあるt検定では同じ人の介入前と介入後の変化量を比較しています。
同じ対象を比較する際にも対応のないt検定を使うとどういう問題があるでしょうか?
実は対応のあるt検定が使える場面で対応のないt検定を使ってしまうと、検出力が落ちてしまいます。
つまり本来は有意差があるのに有意でないと出てしまう可能性が高くなるということです。
それは困りますよね。
対象が同じ群を比較する場合は、必ず対応のあるt検定を使いましょう。
介入前と介入後+αの差をみたい場合
対象が同じで3条件以上の差をみたい場合は以下の手法があります。
- 繰り返しのない二元配置分散分析(データが正規分布している場合)
- フリードマン検定(データが正規分布していない場合)
- コクランのQ検定(データが2値変数の場合)
ここまで解説してきた手法と同様に、比較するデータによって解析手法が違うため当てはまるものを選択しましょう。
“異なる3群以上の差をみたい場合”で説明したように、こちらも多重比較が必要になります。
ただし今回使うのはボンフェローニ調整を使う方法のみです。
具体的には以下の方法で多重比較を行います。
- ボンフェローニ調整をかけて各群間で対応のあるt検定(データが正規分布している場合)
- ボンフェローニ調整をかけて各群間でウィルコクソンの符号順位検定(データが正規分布していない場合)
- ボンフェローニ調整をかけて各群間でマクネマー検定(データが2値変数の場合)
ボンフェローニ調整に関しては”異なる3群以上の差をみたい場合”で説明しているので割愛させていただきます。
データベースを分析する研究(コホート研究)でよく使う統計解析

2つのデータの関係性(相関)をみたい場合
2つのデータの関係性をみたい場合に使うのは相関分析です。
相関分析で使う解析手法は以下の2種類です。
- ピアソンの相関分析(データが正規分布している場合)
- スピアマンの相関分析(データが正規分布していない場合)
文字通り相関を見るための分析で、2種類のデータ間にどれくらい相関があるかを知ることができます。
“相関”という言葉がしっくりこない方もいると思いますので、簡単な例を使って説明しましょう。
例えば身長と体重の関係性をみたいとしましょう。
もちろん身長が高ければ高いほど体重は重くなる傾向があります。
このように片方のデータが大きくなるともう片方のデータも大きくなる場合、正の相関があると言います。
次に小学校の学年と50m走のタイムの関係をみたい場合を考えましょう。
この場合は学年が高ければ高いほどタイムは小さくなるはずです。
片方のデータが大きくなるともう片方のデータが小さくなる場合は、負の相関があると言います。
ちなみに2つのデータに全く関係がない場合は、相関がない(無相関)といいます。
相関分析で注意しなければならないのは、p値(有意かどうか)だけでなく相関係数(十分強い相関があるかどうか)もみる必要があることです。
いくら有意な相関があっても、相関が弱すぎると意味がないからです。
相関係数は-1から1の間の値をとるのですが、以下のように解釈しておけばOKです。
| 相関係数 | 相関の強さ |
|---|---|
| 0.6以上 | 強い正の相関 |
| 0.4~0.6 | 中等度の正の相関 |
| 0.2~0.4 | 弱い正の相関 |
| -0.2~0.2 | ほぼ相関なし |
| -0.4~-0.2 | 弱い負の相関 |
| -0.6~-0.4 | 中等度の負の相関 |
| -0.6以下 | 強い負の相関 |
例外もありますが、ほとんどの研究では中等度以上の相関があった方が望ましいです。
あるものに関連する因子を探索したい場合
たくさんのデータがある場合、どのデータが検証したいものと関連するのか探索したいことがよくあります。
そういったたくさんの変数(説明変数)からあるもの(目的変数)に関連する因子を抽出する解析手法は以下の2種類です。
- 重回帰分析(目的変数が連続値の場合)
- ロジスティック回帰分析(目的変数が2値の場合)
目的変数とは何と関連しているのか知りたいデータです。
たとえばテストの点数に関係する要素を探索する場合、目的変数は”テストの点数”で他の要素は”説明変数”と呼びます。
ちなみに目的変数は従属変数、説明変数は独立変数と呼ばれることもありますが、ほとんど同じ意味です。
この例の場合、テストの点数は連続値なので重回帰分析を使います。
説明変数は連続値でも2値でも構いません。
この目的変数がテストの点数ではなく”大学に進学できるか否か”といった2値変数に変わるとどうなるでしょうか?
その場合はロジスティック回帰分析を使いましょう。
関連する因子を探索する解析手法は以上の2つです。
どちらを使うかの判断も簡単ですよね。
でも重回帰分析とロジスティック回帰分析は使用の制約がかなり多いので注意が必要です。
データ数が一定数以上必要であったり、解析に使う説明変数の数が一定数以下にしなければいけなかったり、など多数の制約があります。
そのため統計解析が初心者のうちは、これらの解析はなるべく避けて方が良いでしょう。
研究デザインを見直すことでなんとかなる場合も多いです。
もしこれらの回帰分析を使う場合は、事前によく調べて知識をつけてから使うようにしましょう。
まとめ

最後におさらいをしましょう。
統計解析手法を選択する際に必要な情報は以下のとおりです。
- 群の差をみたいのか?相関をみたいのか?
- 比較する群の数はいくつか?
- 比較する群の対象者は異なるのか、同じなのか?
- 比較するデータは正規分布しているか?
- 比較するデータは連続変数か2値変数か?
これらの点さえ明確であれば、統計解析手法はすぐに決まるはずです。
まずはこれらの点を明確にするところから始めましょう。
